[最も選択された] 小学算数応用問題の解き方 305362-小��算数応用問題の解き方橋幸一

中古応用自在シリーズ国立私立中学入試突破新版小学算数速さの問題解き方の特訓の落札情報詳細ヤフオク落札価格情報オークフリースマートフォン版

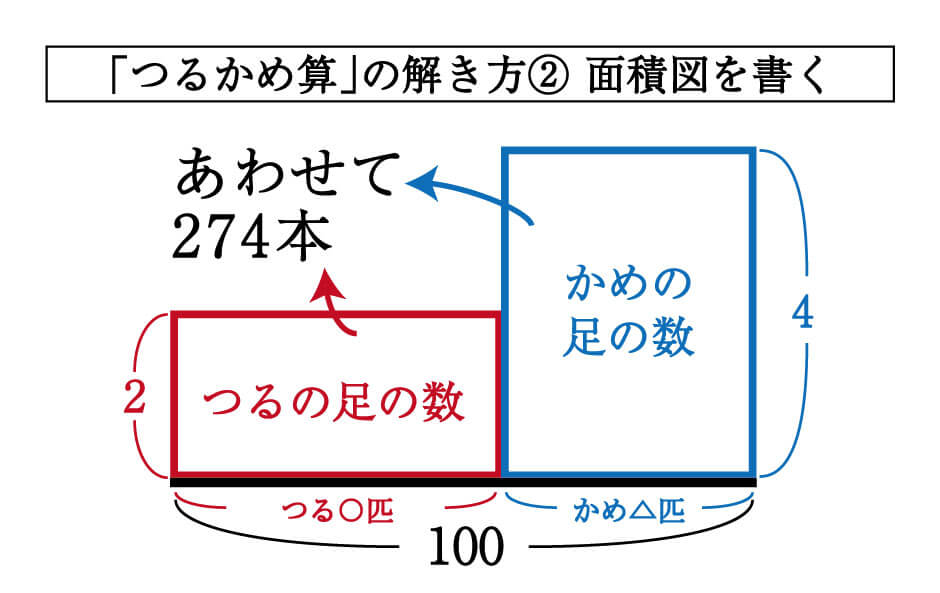
1つ目の解き方は、名づけて「全部つる作戦」。小学生4年生・5年生のみなさんにオススメです（もちろん小学6年生でも有効な解き方）。この方法では、まず「すべてをつるだと考える」ところからスタートします。つるの足は2本。小学算数応用問題の解き方著者橋幸一著出版者法文社出版年月日請求記号 Y3217 書誌ID（国立国会図書館オンラインへのリンク） DOI / 公開範囲国立国会図書館／図書館送信参加館内公開詳細表示資料種別 (materialType) Book

小学算数応用問題の解き方橋幸一

小学算数応用問題の解き方橋幸一-仕事算って？仕事算の練習問題練習問題（1）《解き方》練習問題（2）《解き方》練習問題（3）《解き方》練習問題（4 A × ＝ 50 × 60 A = 3000 ÷ = 150 答え：150g 以上、『『てこ』の問題の公式と解き方』を紹介しました。例題を使うことで簡単に原理を理解することができたと思います。テコの原理の基本となる公式ですのでしっかり覚えて応用問題に挑戦しましょう。

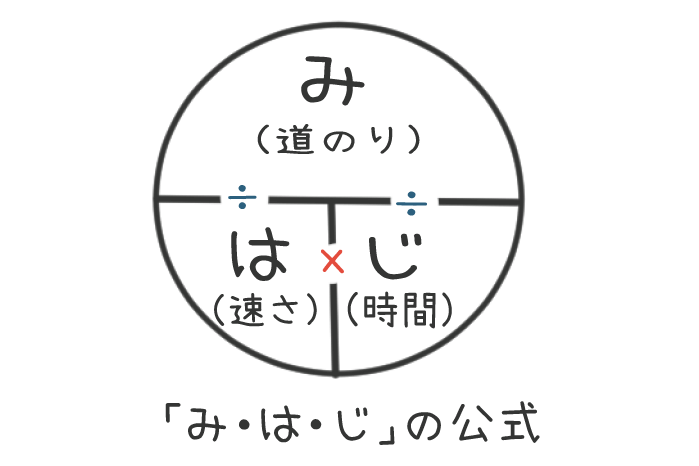
そこで、今回は、算数数学の文章問題が苦手で解けないという人のために解き方のコツと勉強法についてまとめていきたいと思います！ adsense 目次 1 「文章問題が解けない＝国語力不足」ではない！ 2 「集中して読めていない」の対策 3 「解き方の食塩水の問題の解き方小学生・中学受験苦手でも5分で攻略！食塩水の問題を一発で解けるようにする方法（小学生・中学受験用）を説明します。という方は、この記事で攻略可能です！ぜひ最後までご覧ください。食塩水の問題の解き方で覚えるはじめて解くタイプの問題で解き方の方針が分からなくても、図に書いて整理すれば自然と解き方が見えてくると思います。解法は主に2つあるのでそれぞれ見ていきましょう。解法1 Aさんは速さと移動した時間が分かっているので、移動距離も計算できます。時速 5km 5 k m で 15 15 分（ 15 60 15 60 時間）移動したら、 5× 15 60＝125（km） 5 × 15 60 ＝ 125 （ k m ）。 AさんとBさんの

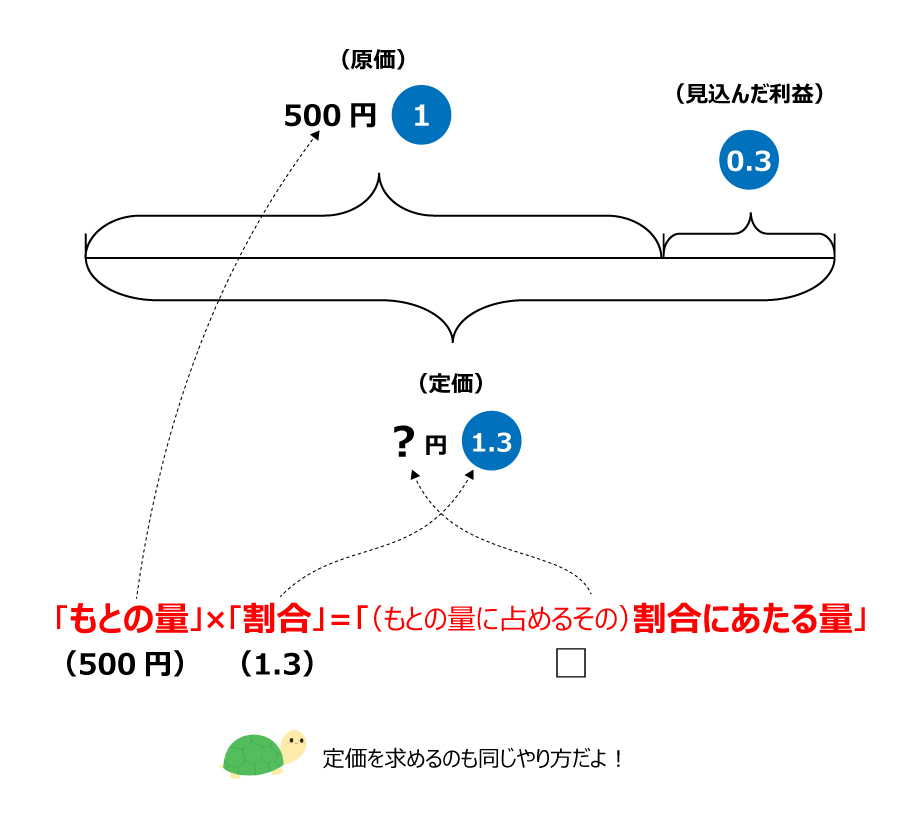
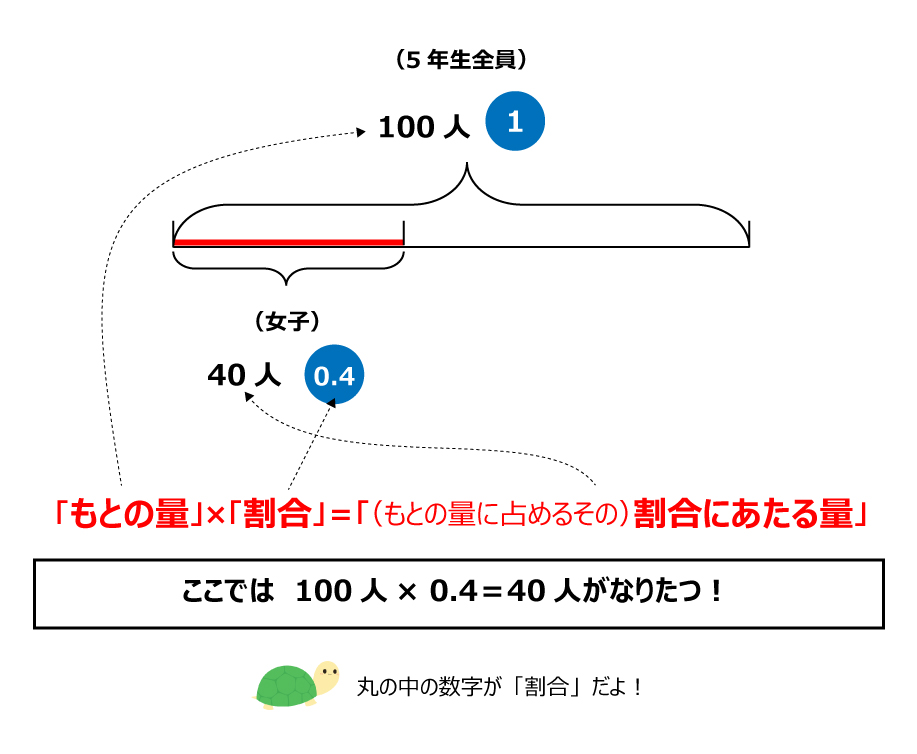
2判断したら、その3パターンの割合の問題を数式に表し、下記にあげた3パターンで解く。 1もとにする量×割合=比べる量 2比べる量÷もとにする量=割合 3比べる量÷割合=もとにする量場合によっては、上記の解き方にこだわらず問題文を数式に表して今回は中学受験をはじめ、算数の文章問題でよく出る仕事算について書いていきたいと思います。 (adsbygoogle = windowadsbygoogle )push({});算数応用問題の解き方(id) 小5です。 5年のカリキュラム出来たら、やるようにと書いてありますが、なかなか〜〜出来ません！！算数は得意な方ですが、やった方がいいのでしょうか？？夏休みの時間のある時も、BASICの宿題で